Welche Schritte sind erforderlich, um den Auslösewinkel des Spritzgießformauswerfers genau zu berechnen?

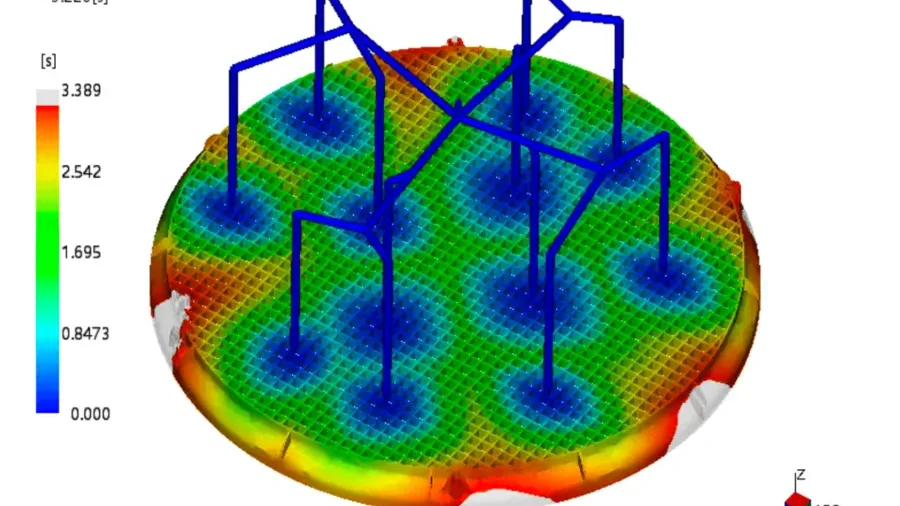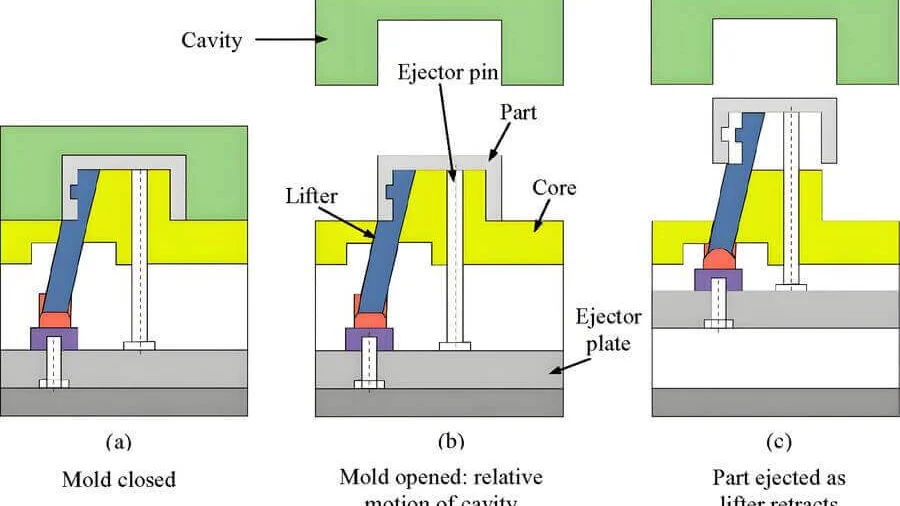
Den idealen Winkel für die Auslösung des Auswerfers beim Spritzgießen zu finden, gleicht jedes Mal einer neuen Herausforderung. Jede Berechnung ist einzigartig.

Um den Auslösewinkel für einen Spritzgussformenauswerfer zu ermitteln, berücksichtigen Sie Faktoren wie Materialschrumpfung, Produkttiefe und Auswerferbewegung. Beachten Sie die Größen- und Formänderungen beim Abkühlen des Materials. Nutzen Sie bewährte Formeln, um einen Winkel zu finden, der ein problemloses Auswerfen des Produkts ermöglicht. Beziehen Sie Materialeigenschaften und die Anforderungen der Konstruktion in Ihre Berechnungen ein.

Die Formel ist nur der Anfang. Jedes Projekt ist anders und erfordert sorgfältige Aufmerksamkeit. Materialien wie Polypropylen verändern die Dinge erheblich. Ich musste einmal die Winkel stark anpassen, um ein Verkleben zu verhindern, da Polypropylen stark schrumpft. Tiefe Designs sind knifflig. Die Tiefe erfordert eine Neuberechnung der Winkel für ein reibungsloses Entformen. Die Überprüfung der Größe und Bewegung des Hebers ist entscheidend. Kleine Details können überraschen. Einmal bewegte sich ein Heber falsch und verursachte beinahe ein Problem. Jetzt überprüfe ich diese Maße immer. Komplexe Formen mögen schwierig erscheinen. Sie in einfachere Teile zu zerlegen, hilft. Es ist wie das Lösen eines Puzzles. Die Verwendung von CAD-Software oder einer Probeform kann spätere Probleme reduzieren.

Wie beeinflussen die Auslösewinkel der Stößel das Spritzgießen?

Die Auslösewinkel von Hebern wirken oft kompliziert. Sie sind jedoch die heimlichen Helden für eine reibungslose Produktentnahme. Durch diese Winkel lassen sich die Produkte problemlos entnehmen. Sie spielen eine wirklich wichtige Rolle.

Der Auslösewinkel des Auswerfers trägt zu einem reibungslosen Entformen beim Spritzgießen bei. Die Materialart beeinflusst diese Winkel. Auch Produktform und -größe spielen eine Rolle. Der Hub des Auswerfers wirkt sich ebenfalls auf die Winkel aus.

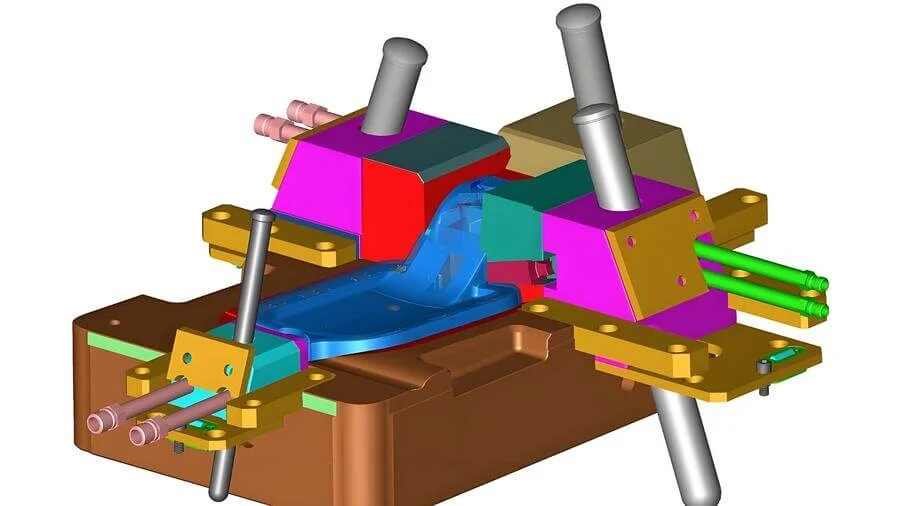
Verständnis der Freigabewinkel der Heber

Der Auslösewinkel des Auswerfers spielt beim Spritzgießen eine entscheidende Rolle, da er das reibungslose Entformen der Produkte ermöglicht. Hauptzweck ist es, ein Anhaften des Produkts am Auswerfer zu verhindern, was sowohl das Produkt als auch die Form beschädigen kann. Die Größe des Auslösewinkels hängt eng mit Faktoren wie Material, Form und Größe des Produkts sowie dem Hub des Auswerfers zusammen.

Materielle Angelegenheiten

Verschiedene Kunststoffe verhalten sich unterschiedlich. Beispielsweise benötigen Materialien mit hoher Schrumpfungsrate wie Polypropylen ( PP ) einen größeren Entformungswinkel, um ein reibungsloses Entformen zu gewährleisten. Typischerweise PP eine Schrumpfungsrate zwischen 1,0 und 2,5 % auf. Für Einsteiger ist es unerlässlich, diese Materialeigenschaften genau zu kennen. Weitere Informationen darüber, wie sich Materialeigenschaften auf die Werkzeugkonstruktion auswirken, finden Sie unter „ Materialeigenschaften beim Spritzgießen¹ ^“ .

Form und Größe des Produkts

Die Geometrie des Produkts beeinflusst den erforderlichen Auslösewinkel maßgeblich. Tiefere Produkte, wie z. B. zylindrische Formen mit einer Tiefe von mehr als 50 mm, erfordern einen größeren Auslösewinkel des Hebers. Eine gängige empirische Formel lautet tan α = S/H, wobei S der horizontale Hub des Hebers und H die Produkttiefe ist. Beispiel: Bei einer Produkttiefe von 100 mm und einem Hub des Hebers von 5 mm gilt:

• H = 100 mm
• S = 5 mm
• Daher ist a≈2,86°.

Um einen sanfteren Austritt zu gewährleisten, sollten Anpassungen vorgenommen werden, um diesen Winkel auf mindestens 3° zu erhöhen.

Anpassungen für komplexe Konstruktionen

Komplexe Formen stellen Herausforderungen an die Berechnungen, da die Abmessungen des Hebers und der Hub berücksichtigt werden müssen. Konstruktionen wie umgekehrte Schnallen lassen sich ohne präzise Werkzeuge oder Software nur schwer genau berechnen.
Zum Beispiel:

• Bei einer Tiefe der umgekehrten Schnalle von 5 mm
• Die horizontale Breite beträgt 20 mm
• Bei einer Hubbreite von 10 mm gilt
  : tan a ≥ 5/(20-10) = 0,5.
  Dies bedeutet: ≥ arctan(0,5) = 26,6°.

Präzise Berechnungen beugen Problemen vor; daher kann der Einsatz von CAD-Software für Simulation und Verifizierung bei komplexen Konstruktionen von Vorteil sein. Erfahren Sie, wie CAD-Software ^die genaue Berechnung dieser Parameter unterstützt.

Durch das Verständnis dieser Prinzipien und Überlegungen kann ein effizientes und fehlerfreies Entformen der Produkte bei Spritzgussverfahren sichergestellt werden.

Wie beeinflussen Materialeigenschaften die Berechnung des Auslösewinkels des Hebers?

Die Materialeigenschaften sind entscheidend für das Verständnis der Auslösewinkel von Auswerfern. Sie beeinflussen die Effizienz und Qualität von Spritzgussteilen. Diese Eigenschaften sind daher von großer Bedeutung.

Materialeigenschaften wie Schrumpfungsrate und Reibungskoeffizient sind von großer Bedeutung. Diese Eigenschaften beeinflussen den Auslösewinkel des Auswerfers. Höhere Schrumpfung erfordert größere Winkel. Auch hohe Reibung bedingt größere Winkel. Größere Winkel verhindern das Festkleben und erleichtern das Entformen.

Materialschrumpfungsraten verstehen

Ich erinnere mich an mein erstes Projekt mit Polypropylen ( PP ). Die Schrumpfungsraten lagen zwischen 1,0 % und 2,5 %. Das lehrte mich, den Entformungswinkel anzupassen. Es war, als würde man Brot backen, ohne zu wissen, wie stark es aufgehen wird. Ohne einen größeren Entformungswinkel wäre es schwierig gewesen, das Produkt sauber aus der Form zu lösen. Es wäre, als würde man einen Aufkleber spurlos abziehen.

Ein zentraler Aspekt bei der Berechnung der Auslösewinkel von Hebevorrichtungen ist das Verständnis der Schrumpfungsrate des Materials³ ^. Materialien wie Polypropylen ( PP ), die für ihre signifikanten Schrumpfungsraten im Bereich von 1,0 % bis 2,5 % bekannt sind, erfordern eine sorgfältige Anpassung der Auslösewinkel.

Reibungskoeffizienten und ihre Auswirkungen

Reibungskoeffizienten können tückisch sein. Das habe ich bei der Arbeit mit klebrigen Materialien gelernt. Sie haften an den Formen wie ein Kleinkind an seinem Lieblingsspielzeug. Hohe Reibung bedeutete, dass ich einen größeren Ablösewinkel benötigte. Ich fand Wege, dieses „Anhaften“ zu reduzieren. Dadurch ließen sich die Produkte problemlos aus den Formen lösen. Es war wie der Abschied alter Freunde nach einer langen Nacht.

Der Reibungskoeffizient eines Materials ist ein weiterer entscheidender Faktor bei der Konstruktion von Formen und Auswerfern, der Anpassungen des Auswurfwinkels für ein reibungsloses Auswerfen erforderlich macht.

Geometrische Überlegungen zu Auslösewinkeln

Geometrie war schon immer meine Stärke. Die Produktentwicklung brachte zusätzliche Komplexität mit sich. Tiefere Produkte mit über 50 mm erforderten spezielle Berechnungen. Die Formel tan α = S/H war dabei sehr hilfreich. Ich verwendete sie für eine zylindrische Konstruktion, bei der der Abwurfwinkel mehr als 3° betragen musste. Es war, als würde man beim Dartspiel den richtigen Treffpunkt finden.

Die Geometrie des Produkts spielt ebenfalls eine wichtige Rolle bei der Bestimmung geeigneter Auslösewinkel, insbesondere bei tieferen Gegenständen, die eine bestimmte Tiefe überschreiten.

Komplexe Schnallenformen meistern

Komplexe Formen fühlten sich an wie das Lösen von Puzzles. Ich zerlegte sie in einfachere Teile, um Winkel zu berechnen. CAD-Software war mir dabei oft eine Hilfe; sie fungierte wie ein treuer Begleiter und zeigte mögliche Kollisionsbedingungen an, die so unberechenbar waren wie Wetterumschwünge.

Bei komplexen Formen müssen Ingenieure diese unter Umständen in einfachere geometrische Formen zerlegen und sich auf CAD-Software-Simulationen ⁴ , um diese Berechnungen zu verfeinern.

Warum sind Produktform und -größe entscheidend für die Bestimmung des Auslösewinkels?

Haben Sie schon einmal einen Kuchen gebacken und hatten Probleme, ihn aus der Form zu lösen? Das ist ähnlich wie bei der Formgebung von Produkten und den damit verbundenen Ablösewinkeln.

Form und Größe des Produkts sind für den Entformungswinkel von großer Bedeutung. Sie beeinflussen maßgeblich, wie leicht sich das Produkt aus der Form lösen lässt. Größere oder komplexere Formen erfordern oft größere Entformungswinkel. Dies beugt dem Anhaften vor. Ein reibungsloser Auswurf ist wichtig.

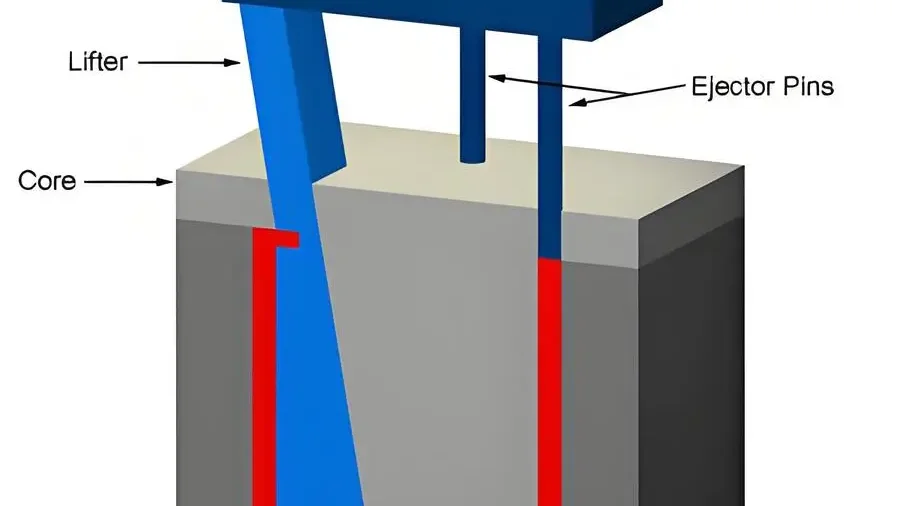
Die Bedeutung des Produktmaterials

Ich erinnere mich noch gut an meine ersten Versuche, zu Hause Kerzen herzustellen. Ich habe verschiedene Wachse ausprobiert und schnell gemerkt, wie wichtig das Material ist. Beim Spritzgießen haben Materialien wie Polypropylen spezifische Schrumpfungsraten und verhalten sich unterschiedlich an Oberflächen. Beispielsweise benötigen Materialien, die stark schrumpfen oder stark reiben, einen größeren Entformungswinkel, damit sie sich beim Entformen nicht verhaken.

Gedanken zu Form und Größe

Denken Sie an die hohen, schlanken Kerzen, die ich hergestellt habe. Bei tiefen Produkten – wie Zylindern mit über 50 mm Durchmesser – muss der Auslösewinkel sorgfältig gewählt werden. Eine hilfreiche Formel berechnet den Winkel anhand der Tiefe H und des Hubs S des Auslösemechanismus. Bei einer Tiefe von 100 mm und einem Hub von 5 mm ergibt sich beispielsweise tan α ≈ 2,86°. Eine Anpassung auf 3° oder mehr kann einen reibungslosen Ablauf gewährleisten.

Komplexe Formen: Berechnungen und Tests

Als ich mit der Herstellung von Seifen mit aufwendigen Mustern begann, zerlegte ich die komplexen Designs in einfachere Teile. Auch im Produktdesign müssen komplizierte Verschlussformen für eine präzisere Winkelberechnung zerlegt werden. Simulationen oder Testformen überprüfen diese Winkel mithilfe von CAD-Tools, um sicherzustellen, dass sie passen, insbesondere bei ungewöhnlichen Formen.

Unter Berücksichtigung der Heberabmessungen

Die Konstruktion von Hebevorrichtungen gleicht einem Puzzle. Es gilt, die einzelnen Teile korrekt anzuordnen. Ihre Größe und Bewegung sind entscheidend. Die Breite w und die horizontale Bewegung s müssen berücksichtigt werden, um Kollisionen beim Auslösen zu vermeiden. Der Auslösewinkel α sollte die Bedingung tan α = h/(bw) erfüllen, um ein reibungsloses Lösen zu gewährleisten. Dies ist besonders wichtig für komplexe Konstruktionen wie umgekehrte Schnallen, bei denen die Winkelberechnungen ⁵ mit der Tragfähigkeit der Hebevorrichtung übereinstimmen müssen.

Wie korrigiere ich die Abmessungen des Hebers und den Bewegungshub?

Haben Sie sich jemals Gedanken darüber gemacht, wie die korrekten Abmessungen der Auswerfer über den Erfolg Ihrer Werkzeugkonstruktion entscheiden? Die richtigen Abmessungen sind entscheidend. Sie bestimmen letztendlich, ob die Konstruktion gelingt oder scheitert.

Die Korrektur der Berechnungen für die Auswerferabmessungen erfordert die Ermittlung des optimalen Auslösewinkels. Dieser hängt vom Material, der Form und dem Hub des Auswerfers ab. Der Auswerfer muss das Produkt reibungslos aus der Form lösen. Dies ist von entscheidender Bedeutung.

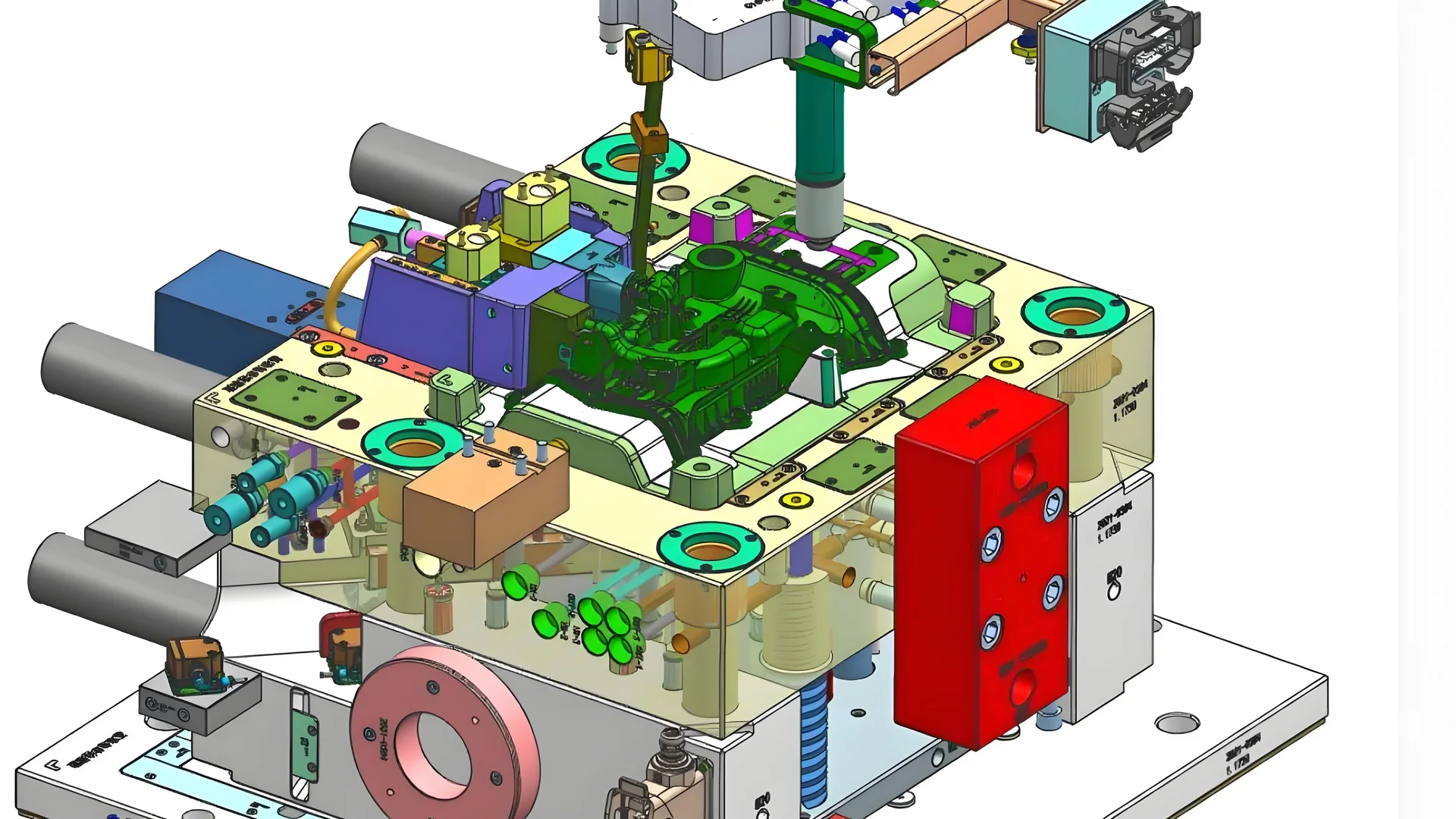
Verständnis der Freigabewinkel der Heber

Als ich mit Formen anfing, merkte ich schnell, wie sehr der Ablösewinkel alles verändert. Es ist wie ein kleiner Trick, der das Herauslösen der Produkte erleichtert. Diesen Winkel zu kennen, ist sehr wichtig, egal ob man mit Polypropylen oder anderen Materialien arbeitet. Stellen Sie sich vor, Sie ziehen einen Aufkleber ab, ohne ihn zu zerreißen – der Winkel ist entscheidend! Bei einfachen Formen oder tiefen zylindrischen Produkten über 50 mm muss der Winkel sorgfältig eingestellt werden.

Der Hauptzweck des Auslösewinkels eines Formhebers besteht darin, ein reibungsloses Entformen des Produkts zu ermöglichen. Dieser Winkel ist entscheidend, da er die Qualität des sich nach dem Spritzgießen lösenden Produkts beeinflusst. Der Auslösewinkel hängt von verschiedenen Faktoren ab, darunter Material, Form und Größe des Produkts sowie der Hub des Formhebers.

Berechnung der Auslösewinkel für verschiedene Formen und Materialien

Ich habe einmal mit Materialien gearbeitet, die stark schrumpften. Die Lösung, um Anhaften zu vermeiden, war die Anpassung des Ablösewinkels. Es ist wie beim Kochen – verschiedene Materialien erfordern unterschiedliche Einstellungen. Tiefere Produkte oder solche mit hoher Reibung benötigen einen größeren Winkel. Die perfekte Balance zu finden, ist ungemein befriedigend; es ist, als würde man einen perfekt gebackenen Kuchen aus dem Ofen holen!

Verschiedene Kunststoffe weisen unterschiedliche Schrumpfungsraten und Reibungskoeffizienten auf. Bei Produkten aus stark schrumpfenden Materialien kann ein größerer Ablösewinkel das Anhaften verhindern. Auch tiefere Produkte erfordern größere Ablösewinkel.

Wenn Sie beispielsweise ein zylindrisches Produkt mit einer Tiefe von mehr als 50 mm haben, könnten Sie den Auslösewinkel wie folgt berechnen:

tan a = S/H

Dabei stellt S den horizontalen Hub des Hebers dar.
In der Praxis dieser Winkel ⁶ üblicherweise nicht kleiner als 3° sein.

Korrektur der Berechnungen unter Berücksichtigung der Stößelabmessungen und des Hubs

Nun zu den Abmessungen des Hebers und seinem Hub – wichtige Aspekte beim Formen. Einmal funktionierte ein Heber nicht richtig, weil seine Breite nicht zur Schließe passte. Mir wurde klar, dass die exakte Übereinstimmung dieser Abmessungen Probleme vermeidet.

Berücksichtigen Sie neben den Produkteigenschaften auch die Abmessungen und die Bewegungsabläufe Ihres Hebers:

• Nehmen wir an, Ihr Heber hat eine Breite w und bewegt sich horizontal mit einem Hub s.
• Stellen Sie sicher, dass, wenn die Breite w Ihres Hebers kleiner ist als die horizontale Breite b der Schließe, der Bewegungshub ein vollständiges Auskuppeln von der Schließe ermöglicht.
• Der Auslösewinkel ⁷ muss möglicherweise folgende Bedingung erfüllen:
  tan a≥ h/(bw)

Wie kann ich komplexe Schnallenformen in Winkelberechnungen berücksichtigen?

Haben Sie sich jemals über komplexe Schnallenformen bei Winkelberechnungen gewundert? Damit sind Sie nicht allein! Entdecken Sie diese einfachen Strategien. Mit diesen Tipps wird es Ihnen bestimmt leicht fallen.

Komplexe Schnallenformen lassen sich zur Winkelberechnung in einfache geometrische Elemente unterteilen. Der Auslösewinkel jedes Elements wird bestimmt, der größte Wert dient als Standard. CAD-Software-Simulationen können diese Winkel präziser anpassen.

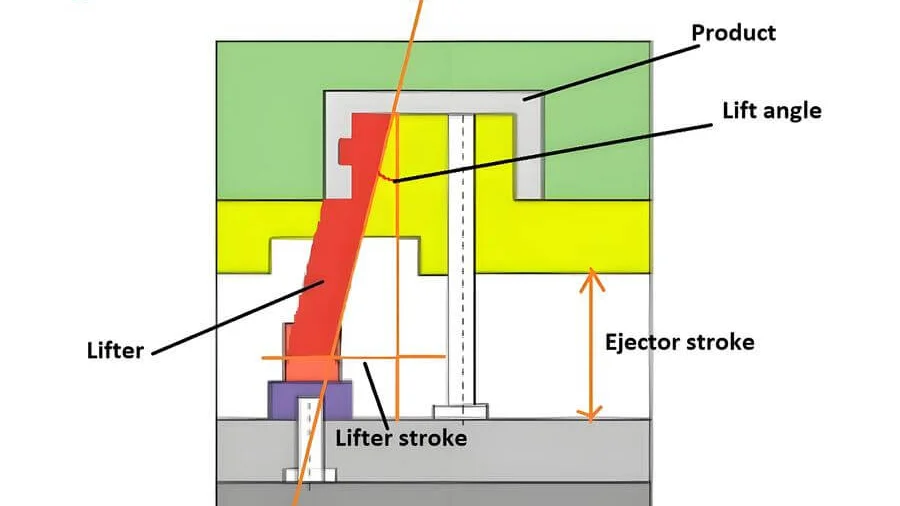
Grundlegende Prinzipien verstehen

Ich erinnere mich noch gut an das erste Mal, als ich ein Produkt problemlos aus der Form lösen wollte. Es war, als würde man einen verhedderten Wollknäuel entwirren – verwirrend und ärgerlich. Doch die Erkenntnis, dass der Auslösewinkel des Formhebers die Lösung war, hat mir die Augen geöffnet. Dieser Winkel ist wichtig, weil er vom Material, der Form, der Größe des Produkts und sogar von der Bewegung des Formhebers abhängt.

Das Hauptziel der Winkelberechnung bei komplexen Schnallenformen ist die Gewährleistung einer reibungslosen Produktentformung. Dies erfordert die Berücksichtigung von Faktoren wie Materialeigenschaften und dem Entformungswinkel des Auswerfers. Die Größe des Entformungswinkels hängt vom Material, der Form und Größe des Produkts sowie vom Hub des Auswerfers ab. Daher ist es entscheidend, den Ansatz an die spezifischen Produktanforderungen anzupassen.

Material- und Formüberlegungen

PP beispielsweise schrumpft stark und benötigt daher einen größeren Ablösewinkel. Das ist vergleichbar mit dem Herauslösen eines klebrigen Kuchens aus der Form; für ein sauberes Herauslösen ist der richtige Winkel entscheidend. Produkte mit tiefen Hohlräumen erfordern spezielle Berechnungen, beispielsweise zylindrische Gegenstände mit einer Tiefe von über 50 mm.

Materialeigenschaften wie die Schwindungsrate beeinflussen die Winkelberechnungen maßgeblich. Beispielsweise können Materialien mit höherer Schwindung größere Entformungswinkel erfordern. In solchen Fällen ist die Verwendung empirischer Formeln unerlässlich:

tan a = S/H,
wobei S die horizontale Bewegung und H die Tiefe ist.

Bei einer Produkttiefe von 100 mm und einem Hub von 5 mm ergibt sich
tan α = 5/100 = 0,05,
was einem Winkel von ca. 2,86° entspricht. Eine Erhöhung dieses Winkels auf mindestens 3° gewährleistet ein reibungsloseres Entformen.

Korrigierte Berechnungsmethoden

Bei der Berücksichtigung von Abmessungen und Bewegungsabläufen wird es knifflig. Der Heber darf die Verriegelung beim Abnehmen nicht behindern – eine Lektion, die ich gelernt habe, als ich mich verrechnet hatte und einen Abschnitt neu anfertigen musste.

Bei komplexen Formen ist es unerlässlich, sowohl die Abmessungen des Hebers als auch seinen Hub zu berücksichtigen:
tan α ≥ h/(b – w) ist hier entscheidend.
Beispiel:
Tiefe der umgekehrten Schnalle = 5 mm,
Schnallenbreite = 20 mm,
Heberbreite = 10 mm,
der Winkel muss α
≥ 26,6°
oder anhand der Hublänge überprüft werden.
Die Anwendung dieser Regel bewahrte mich vor einem weiteren Fehler.

Umgang mit komplexen Schnallenformen

Komplexe Schnallen mit Kurven oder ungewöhnlichen Formen gleichen Puzzles – man sollte sie in einfache Formen zerlegen und jeden Auslösewinkel separat mit den zuvor genannten Methoden berechnen.
Simulationswerkzeuge wie CAD-Software sind für die Überprüfung dieser berechneten Winkel unerlässlich – sie dienen als zusätzliches Augenpaar und decken Fehler auf, die mir möglicherweise entgehen.
Diese Werkzeuge können Interferenzbedingungen vorhersagen, die in Vorentwürfen nicht ersichtlich sind, und ermöglichen so Anpassungen, die die Funktionalität und die Einhaltung der technischen Normen gewährleisten.
Für weitere Einblicke, wie Simulationswerkzeuge die Konstruktionsgenauigkeit verbessern können, oder um mehr über empirische Formeln für Winkelberechnungen zu erfahren ^, wird ^eine weiterführende Recherche empfohlen.

Abschluss

Bei der Berechnung der Auslösewinkel beim Spritzgießen müssen Materialschrumpfung, Produkttiefe und Auslösebewegung berücksichtigt werden, um ein reibungsloses Entformen ohne Anhaften zu gewährleisten.